تحاليل البقاء على قيد الحياة

بسم الله الرحمن الرحيم
السلام عليكم ورحمة الله وبركاته

محاضرة رقم 258/2020 – تحاليل البقاء على قيد الحياة

دكتور الدرديري فضل إبراهيم فضل

في دراسات السرطان ، تكون الأسئلة البحثية النموذجية مثل:
ما هو تأثير بعض الخصائص السريرية على بقاء المريض ؟
ما هو احتمال بقاء الفرد على قيد الحياة لمدة 3 سنوات؟
هل هناك اختلافات في البقاء على قيد الحياة بين مجموعات المرضى؟
يتوافق تحليل البقاء مع مجموعة من الأساليب الإحصائية المستخدمة للتحقيق في الوقت الذي يستغرقه حدوث حدث مثير للاهتمام.
يستخدم تحليل البقاء في مجموعة متنوعة من المجالات مثل:
دراسات السرطان لتحليلات وقت بقاء المرضى .
وعلم الاجتماع من أجل ‘تحليل تاريخ الأحداث’.
وفي الهندسة من أجل ‘تحليل وقت الفشل’.
محتويات
الأهداف
مفاهيم أساسية
وقت البقاء على قيد الحياة ونوع الأحداث في دراسات السرطان
الرقابة
وظائف النجاة والمخاطر كابلان ماير
تقدير البقاء على قيد الحياة تحليل البقاء في R
تثبيت وتحميل حزمة R المطلوب
أمثلة على مجموعات البيانات
حساب منحنيات البقاء على قيد الحياة: survfit ( )
الوصول إلى القيمة التي أرجعها survfit ( )
تصور منحنيات البقاء على قيد الحياة
جدول حياة كابلان ماير: ملخص منحنيات البقاء على قيد الحياة
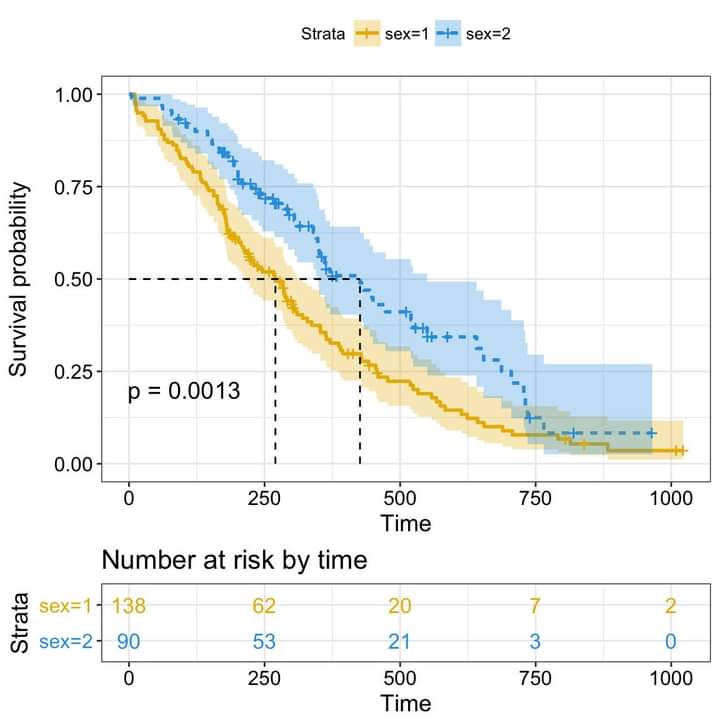
اختبار رتبة اللوغاريتم الذي يقارن منحنيات البقاء على قيد الحياة: survdiff ()
تناسب منحنيات البقاء المعقدة
ملخص
المراجع
الأهداف
الهدف من هذا الفصل هو وصف المفاهيم الأساسية لتحليل البقاء. في دراسات السرطان ، تستخدم معظم تحليلات البقاء الطرق التالية:
مخططات كابلان ماير لتصور منحنيات البقاء اختبار لوغاريتمات الترتيب لمقارنة منحنيات البقاء على قيد الحياة لمجموعتين أو أكثر من انحدار المخاطر النسبية لكوكس لوصف تأثير المتغيرات على البقاء.
تمت مناقشة نموذج كوكس في الفصل التالي:
نموذج كوكس للمخاطر النسبية.
هنا ، سنبدأ بشرح المفاهيم الأساسية لتحليل البقاء على قيد الحياة ، بما في ذلك:
كيفية إنشاء وتفسير منحنيات البقاء على قيد الحياة ،
وكيفية تحديد واختبار اختلافات البقاء على قيد الحياة بين مجموعتين أو أكثر من المرضى.
بعد ذلك ، سنستمر في وصف التحليل متعدد المتغيرات باستخدام نموذج كوكس للمخاطر النسبية.
مفاهيم أساسية
هنا ، نبدأ بتحديد المصطلحات الأساسية لتحليل البقاء بما في ذلك:
وقت البقاء والحدث
الرقابة
وظيفة البقاء على قيد الحياة ووظيفة الخطر
وقت البقاء على قيد الحياة ونوع الأحداث في دراسات السرطان هناك أنواع مختلفة من الأحداث ، بما في ذلك:
الانتكاس
التقدم
الموت
عادة ما يسمى الوقت من ‘الاستجابة للعلاج’ (مغفرة كاملة) لحدوث الحدث موضع الاهتمام وقت البقاء (أو الوقت للحدث).
أهم مقياسين في دراسات السرطان هما:
(1) الوقت حتى الموت.
و 2) فترة البقاء على قيد الحياة الخالية من الانتكاس ، والتي تتوافق مع الوقت بين الاستجابة للعلاج وتكرار المرض.
يُعرف أيضًا باسم فترة البقاء على قيد الحياة الخالية من الأمراض ووقت البقاء على قيد الحياة بدون أحداث.
الرقابة
كما ذكر أعلاه ، يركز تحليل البقاء على المدة المتوقعة من الوقت حتى وقوع حدث مثير للاهتمام (الانتكاس أو الموت). ومع ذلك ، قد لا يتم ملاحظة الحدث لبعض الأفراد خلال فترة الدراسة ، مما ينتج عنه ما يسمى بالملاحظات الخاضعة للرقابة.
قد تنشأ الرقابة بالطرق التالية:
1- لم يختبر المريض (حتى الآن) حدثًا مثيرًا للاهتمام ، مثل الانتكاس أو الوفاة ، خلال فترة الدراسة ؛
2- فقدان المريض للمتابعة خلال فترة الدراسة.
3- يمر المريض بحدث مختلف يجعل المتابعة الإضافية مستحيلة.
هذا النوع من الرقابة ، المسمى بالرقابة الصحيحة ، يتم التعامل معه في تحليل البقاء.
وظائف البقاء والخطر
يتم استخدام احتمالين مرتبطين لوصف بيانات البقاء:
احتمال البقاء على قيد الحياة واحتمال الخطر. ا
حتمال البقاء ، المعروف أيضًا باسم وظيفة الناجي(S(t، هو احتمال بقاء الفرد على قيد الحياة من الأصل الزمني (مثل تشخيص السرطان) إلى وقت مستقبلي محدد.
الخطر ، المشار إليه بواسطة( h (t، هو احتمال أن يكون للفرد الذي يخضع للمراقبة في وقت t حدث في ذلك الوقت.
لاحظ أنه على عكس وظيفة الناجي ، والتي تركز على عدم وجود حدث ، فإن وظيفة الخطر تركز على الحدث الذي يقع.
تقدير بقاء كابلان ماير إن طريقة كابلان ماير (KM) هي طريقة غير معلمية تستخدم لتقدير احتمالية البقاء على قيد الحياة من أوقات البقاء المرصودة (كابلان وماير ، 1958). يتم حساب احتمال البقاء على قيد الحياة في الوقتti) ، S (ti) i) ، على النحو التالي:
S(ti)=S(ti−1)(1−dini)S(ti)=S(ti−1)(1−dini)
Where,
S(ti−1) = the probability of being alive at ti_1
ni = the number of patients alive just before ti
di= the number of events at ti
t0= 0, S(0) = 1
الاحتمال المقدر ((S (t)هو دالة خطوة تغير القيمة فقط في وقت كل حدث. من الممكن أيضًا حساب فترات الثقة لاحتمالية البقاء. يوفر منحنى البقاء KM ، وهو مخطط لاحتمال بقاء KM مع مرور الوقت ، ملخصًا مفيدًا للبيانات التي يمكن استخدامها لتقدير التدابير مثل متوسط ​​وقت البقاء.